https://www.acmicpc.net/problem/10830
10830번: 행렬 제곱
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
분할 정복
1부터 n까지의 합을 재귀를 이용하면 n번 연산을 하게 된다.
여기서 n을 2로 나누어
$$ sum() = 1+2+..+n $$
$$ =(1+2+...+\frac{n}{2}) + ((\frac{n}{2}+1)+...+(\frac{n}{2}+\frac{n}{2}) $$
$$ =( \frac{n}{2} \times \frac{n}{2} + sum( \frac{n}{2} ) &&
$$ sum(n)=2 \times sum(\frac{n}{2}) + \times \frac{n^{2}}{4} && (n 짝수일 경우)
이 아이디어를 이용해서 행렬도 분할 정복할 수 있다.
행렬 분할 정복
$$ A^{m} = A^{m/2} \times A^{m/2} $$
m이 홀수일 경우에는
$$ A^{m} = A \bullet A^{m-1} $$
재귀를 이용하여 순서를 본다면
ex) m = 30
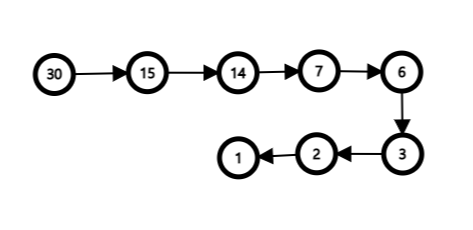
짝수일 경우 2로 나누고, 홀수일 때는 -1을 해주어 최종 1이 나올 때까지 재귀하여 결과를 구한다.
코드
#include <bits/stdc++.h>
#define MAX_N 5
using namespace std;
int n;
long long b;
// matrix = 행렬 원본, temp = 제곱 중 행렬
vector matrix(MAX_N, vector<int>(MAX_N, 0));
vector<vector<int> > temp;
//행렬의 곱셈
vector<vector<int> > matrix_mult(vector<vector<int> >m_1, vector<vector<int> > m_2) {
vector result(MAX_N, vector<int>(MAX_N, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
result[i][j] += (m_1[i][k] % 1000) * (m_2[k][j] % 1000);
}
}
}
return result;
}
// 거듭제곱 재귀이용
vector<vector<int> > pow(long long m) {
//홀수일 때
if (m == 1) return matrix;
if (m % 2 > 0) return matrix_mult(pow(m-1), matrix);
vector<vector<int>> pow_m = pow(m / 2);
return matrix_mult(pow_m, pow_m);
}
int main(void) {
cin >> n >> b;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
temp = pow(b);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << temp[i][j] % 1000 << " ";
}
cout << '\n';
}
}
입력받는 b의 크기가 int 형 변수의 크기를 넘어가기에 long long으로 선언하고,
행렬 곱이 많이 커질 것을 대비하여 1000의 나머지로 곱셈하도록 하였다.
위에 두가지만 조심한다면 단번에 해결 가능할 것이다.
'알고리즘 > 분할 정복' 카테고리의 다른 글
| (c++) BOJ 11401번: 이항 계수 3 (1) | 2024.01.14 |
|---|---|
| (c++) BOJ 1629번: 곱셈 (0) | 2024.01.13 |
| (c++) BOJ 1780번: 종이의 개수 (1) | 2024.01.13 |
| (c++) BOJ 2630번: 색종이 만들기 (0) | 2024.01.12 |
| (c++) BOJ 11444번: 피보나치 수 6 (0) | 2024.01.12 |

댓글